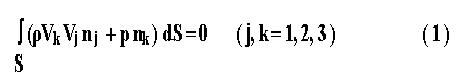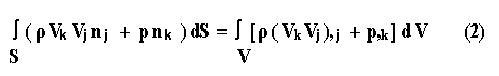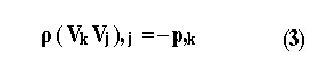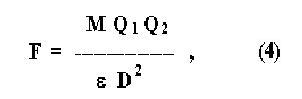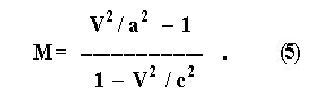Вы можете в режиме он-лайн дискуссии на форуме представить свои мнения о настоящем рассказе, а также оставить комментарии для публикации на настоящей странице.

Популярное предисловие Представьте ванну, наполненную водой. Мы открываем пробку: с бурлением, завихрениями и плеском пузырей в стоке вода начнет выливаться. Как узнать, сколько ее вытекает за минуту и какие скорости частиц воды в стоке ? Ну, скажете вы, первое  легко замерить, подставив снизу емкость с водой, а  вот скорости частиц описать и измерить очень трудно Но можно поступить иначе: замерить - на сколько уменьшится толщина слоя воды за одну минуту, а потом умножить этот результат на площадь ванны – вот и вытекший объем за это время; также легко посчитать и среднюю скорость частиц. Как видно, для вычисления физических характеристик можно использовать данные не только в том месте, где происходят самые сложные процессы, и ясно, что мы сами можем выбирать любую поверхность, по которой можем посчитать важные характеристики такого стока, как в ванне. Этот пример может служить простой иллюстрацией к понятию инвариантного интеграла: суммарное (или интегральное) изменение одних физических характеристик по произвольной замкнутой вокруг особого объекта (такого как, сток в ванной) поверхности позволяет найти другие физические характеристики этого особого объекта. Это справедливо также, например, для распространения тепла или света: характеристики источников/ стоков тепла или света можно найти с помощью интегрирования по произвольной поверхности (а в случае задач, в которых важны только две переменные--- по произвольному контуру). И не обязательно знать точно, что происходит в непосредственной близи от особого объекта. Потому что там нужно очень точное математическое описание сложнейших полей, а решаемые упрощенные модели для получаются только для условных точечных объектов. Самой древней проблемой науки является проблема разрушения и прочности. Эту проблему начинал решать ещё первобытный человек, разбивая камни, чтобы делать из них ножи, или выбирая крепкую дубину в качестве оружия. Однако до сих пор эта проблема не решена, о чём говорят многочисленные, непредвиденные разрушения мостов, зданий, инструментов. Сложность проблемы объясняется загадочным и капризным поведением трещин, поскольку разрушение есть процесс роста трещин, а точнее, процесс распространения фронта трещины или её конца, если посмотреть в разрезе. Именно в кончике трещины происходят сложные явления поглощения энергии. И вот, когда в середине 20-ого века тысячи ученых и инженеров были заняты решением проблемы разрушения, молодой математик из Советского Союза Геннадий Черепанов предложил интегральную характеристику сложных процессов в кончике трещины в форме контурного интеграла, основанного на законе сохранения энергии. И встретил … ожесточенное сопротивление при ее опубликовании, так что только в 1967 г. его статья с этим результатом была опубликована в ведущем в СССР журнале по механике «Прикладная математика и механика», где фамилия "Г.П.Черепанов" стояла в титуле, как принимающего участие в издании журнала.  Законы сохранения массы, энергии, заряда, количества движения, момента количества движения и другие являются основой общепринятых дифференциальных уравнений классической физики, решение которых дало ключ многим приложениям науки на практике. Инвариантные интегралы позволяют выразить те же законы сохранения в форме контурных или поверхностных интегралов, инвариантных относительно, т.е. не зависящих от, контура или поверхности интегрирования.  Из инвариантного интеграла, дающего глобальную формулировку проблемы, можно вывести локальные, дифференциальные уравнения, но инвариантный интеграл содержит больше возможностей, чем соответствующие дифференциальные уравнения, - он допускает решения, которые в отдельных точках поля бесконечны.  Эта лишняя возможность может быть использована для решения критических проблем, выходящих за рамки дифференциальных уравнений. Вообще-то в физике немало объектов, свойства которых очень сложно изучать близ их самих. Проблема разрушения материалов и конструкций является наиболее важной проблемой такого типа, для решения которой недостаточно одних дифференциальных уравнений, даже сколь угодно точных. Именно такой инвариантный  интеграл был построен Г.П. Черепановым применительно к проблемам разрушения.  Обобщенный интеграл позволил найти параметры еще многих особенностей разных физических полей, для которых непосредственное понимание особенности почти невозможно. Его открытие было подхвачено на Западе и развито под именем  J – интеграла в тысячах работ сотен западных учёных, не пожелавших  ссылаться на работы, написанные на русском языке.  Хотя работа американца J.Rice только подробно обосновывала  свойство независимости от контура интегрирования интеграла, введенного Г.Черепановым. Но именно статья J.Rice с исследованием интеграла Черепанова, а не сама первичная работа, стала одной из самых цитируемых статей в науке 20 века.  Очерк  «К истории инвариантного интеграла» рассказывает об истории открытия для профессионального читателя, а мемуар «Воспоминания», написанный для широкой публики, помогает  понять социальных и личностных мотивы, тесно связанные с  этим открытием. Они взаимосвязаны и потому публикуются вместе.  Программа ИНК дает возможность профессионалам и начинающим исследователям познакомиться с подлинниками основных публикаций Г.П.Черепанова об инвариантных интегралах. В дополнительном файле по ссылке вы найдете выходные данные монографий и журнальных статей на русском и английском языках и сможете скачать PDF-версии самих работ, с современными комментариями автора и исправленными опечатками.   Уместно упомянуть, что позже Г.П. Черепанов вывел инвариантные интегралы для электромагнитных, тепловых, гравитационных и других полей. И доказал с их помощью ряд классических формул и  получил новые результаты.   Инвариантный интеграл  был использован, например, при выводе нового закона - обобщённого закона Кулона для движущихся зарядов, где при скоростях, больших скорости света в среде, принципиально меняется характер их взаимодействия. Впрочем, надо понимать, что законы сохранения справедливы лишь в определённых границах. Например, масса m может превратиться в тепло и световую волну (луч света) с энергией mc2, где с — скорость света, что наблюдается в радиоактивных превращениях, используемых в атомной энергетике и военном деле (атомное и водородное оружие). В настоящее время лишь закон сохранения энергии претендует быть абсолютным. А.А. Борзых

К ИСТОРИИ ИНВАРИАНТНОГО ИНТЕГРАЛА Г. П. Черепанов (Пр.1) Honorary Life Member of the New York Academy of Sciences История инвариантных (т.е. не зависящих от пути интегрирования) интегралов насчитывает более 200 лет. Такие интегралы встречались еще в работах Эйлера. Коши и Риман разработали инвариантные интегралы в теории функций комплексного переменного для проблем гидродинамики несжимаемой идеальной жидкости, Максвелл -- для проблем электромагнитного поля, Эшелби — для физической теории дислокаций(1951), Нетер связала инвариантные интегралы с вариационными принципами . Черепанов вывел инвариантный интеграл для механики разрушения, динамики и статики сплошных сред и, в частности, твердых упруго-пластических материалов(1967), Райс доказал его инвариантность для статики нелинейно-упругих материалов в теории концентрации напряжений (1968). Совпадающие интегралы Эшелби и Райса являются частными случаями интеграла Черепанова. В настоящей заметке излагаются некоторые вопросы, связанные с открытием инвариантного интеграла механики разрушения. “The path-independent integral was discovered independently around the same time by Genady Cherepanov of Moscow”, признался Джеймс Райс в своей речи в 1994 году при получении медали и премии Тимошенко за открытие инвариантного,т.е. не зависящего от пути интегрирования , интеграла, который в механике разрушения был получен впервые автором настоящей заметки в 1967 году [1] (термин «инвариантный» был введен мною позже). Другую премию за этот интеграл Райс получил еще в 1970 году. Статья Райса [2], опубликованная в 1968 году и считающаяся его главным научным достижением, была представлена в печать через два месяца после появления журнала ПММ со статьей Черепанова в библиотеках ведущих университетов США. Без всякой ссылки на первоисточник мой интеграл появляется в самом начале статьи Райса, посвященной его доказательству при помощи теоремы Гаусса-Остроградского.(Если бы я дал такое доказательство в своей статье, думаю, никто не обратил бы на него внимание. К счастью, это сделал Райс.) В моей статье [1] эта инвариантность вытекает из самого метода и является очевидным следствием закона сохранения энергии, в связи с чем в моей статье [3], опубликованной раньше статьи [2], в качестве пути интегрирования, кроме окружности, используется также прямоугольный контур. Подробнее см. статьи [4-8].

.

"Воспоминания" в более удобном формате и с примечаниями можно прочитать отдельно по ссылке ВОСПОМИНАНИЯ Г. П. Черепанов       В детстве я был хулиган и дружил больше с хулиганами, с культурными людьми, за исключением Валерки Колпакова, дружбы у меня как-то не получалось. Мое приобщение к культуре началось со второго класса, когда моя молодая красивая учительница погладила меня по голове ( см. рассказ Гены Чера «Моя первая учительница»). Следующий человек, который повлиял на мое мировоззрение, был Николай Иванович, учитель математики в 5-омклассe. Прикладываю чудом сохранившееся фото учеников 5-ого класса мужской школы № 107 г. Горького: морщинистый человек в середине—Николай Иванович ( справа от него сидит его любимчик, Гена Черепанов). Вероятно, он подарил это фото маме бесплатно, так как вряд ли у нее нашлись бы деньги заплатить. Целый год он поручал мне проводить все уроки (лишь давал тему и примерное место в учебнике), а сам дремал за столом и следил за дисциплиной. Я был очень горд с тех пор и потом за все годы в школах (с 7-ого по 10-ый класс я учился в сельской школе г. Меленок) никогда не поднимал руки. Учителя это знали и, когда уже больше никто не мог ответить на какой-нибудь трудный вопрос или задачу, обычно поднимали меня:     « Ну, ладно. Давай, Черепанов!» И они ошибались редко (я не помню таких случаев).       Но, впоследствии мне пришлось поплатиться за это дурное воспитание и плохие привычки. Академик Ржевский выгнал меня из Горного за то, что я поручал читать свои лекции своим студентам.  Позже такая история повторилась в Америке: в FIU мне надоело читать одни и те же лекции  и я поручал их  читать своим студентам. До сих пор считаю это правильной практикой---все эти студенты, и в России , и в Америке, стали профессорами. Преподавательская работа профессора не требует большого интеллекта и по силам почти каждому студенту. А главное влияние на меня в детстве, конечно, оказала мама, как и у всех людей. Она была человеком гордым, независимым, но совершенно неприспособленным к жизни, как я понял много позже, уже будучи взрослым. Отец погиб на войне, но мама не верила в его смерть и ждала его еще лет 20 позже. Жизнь без дома,  без каких-либо средств существования, без какой-либо помощи, с двумя малыми детьми на руках  и категорически не уметь кланяться или просить---я сейчас не могу представить, как мы выжили. « Мы — не нищие», частенько говорила она. Сушеная морковь вместо сахара и печеная в золе луковица были  тогда лакомством.  С тех пор, неумение просить чего-либо и неприхотливость вошли в мою кровь и плоть. Моим школьным и последующим успехам она никогда не удивлялась — она  считала, что иначе и быть не могло. Я сам так считал всегда и только недавно понял почти невероятную, фантастическую случайность своих сравнительных успехов.

И все-таки это признание является исключительным явлением, хотя Джим нигде не цитирует мои работы, чтобы не давать примера другим. Райс — общепризнанный гений Америки, поразительно честный человек, что необычно для ученого такого масштаба. Я испытываю к нему благодарность за это признание. Это — настоящая милость с его стороны. Он мог бы и не признавать этого вовсе — именно так и поступило бы абсолютное большинство его западных коллег. Почему? Потому что престиж российской науки чрезвычайно низок на Западе и, в особенности, в США, Англии и Германии. Считается неприличным цитировать научную статью, написанную русским человеком. («Читать их очень трудно. Или никому не нужная схоластика или бред, замаскированный формулами. Почти одни теоретические рассуждения, эксперименты—примитивны или неоригинальны», примерно так объяснил мне один американский профессор. Речь шла о статьях русских авторов на английском языке, опубликованных или переведенных на Западе.) Поэтому русскую работу цитируют только после того, как кто-то из известных американских ученых признал ее. Таким образом, после того как Макс Вильямс, Джим Райс, Джордж Ирвин, Джок Эшелби и другие общепризнанные авторитеты признали работу [1], она стала классической и иногда цитируемой, в то время как другие мои статьи и книги, гораздо более достойные признания, цитируются редко, а молчаливое списывание их результатов и идей является массовым явлением. Иначе говоря, сравнительный успех этой работы — чистая случайность, стечение некоторых благоприятных обстоятельств. Райс как ученый вырос в эпоху после запуска русского Спутника, на который Америка среагировала фантастическим финансированием науки, когда русская наука — по существу, небольшая кучка честных ученых мирового класса — стала предметом внимания и подражания ( что уже через 20 лет сменилось обычным презрительным невниманием). Сам Райс, по его собственному признанию, изучал тогда русский язык, чтобы читать статьи Черепанова. Таким образом, «спутниковый» прорыв русской науки сыграл большую роль в признании работы [1]. Сегодня никто не изучает русский язык, чтобы прочесть свежую статью российского ученого, а Райс со стыдом вспоминает это увлечение юности.

.

"Воспоминания" Г.Черепанова в более удобном формате можно прочитать отдельно по ссылке       Что и говорить — то было трудное время для всего народа. Сначала самая кровопролитная война в истории человечества, потом американская политика удушения ослабленной войной  России голодом и постоянная угроза интервенции. Советская историография совершенно неверно представляла эту войну как войну с Германией, или с сумасшедшим недоноском Гитлером, или с фашизмом. Все это сознательно УМАЛЯЛО подвиг русского народа. В 1941 году на Россию напала почти вся Европа, объединенная организационным, политическим и военным гением Гитлера под знаменем фашизма. Практически все нации Европы отдались Гитлеру без сопротивления и за все время войны никаких движений сопротивления, за исключением Сербии Тито, НЕ БЫЛО. В армии завоевателей , кроме немцев, служили итальянцы, испанцы, венгры, чехи, румыны, хорваты, литовцы,  латыши, эстонцы,словаки, болгары, поляки, датчане, голландцы, бельгийцы, французы. Вся промышленность Европы работала против России! Это была война Европы с Россией! Сознательное искажение истории того времени было нужно как США (умалить подвиг России), так и России, которая взяла на себя после войны неразрешимую задачу перевоспитания завоеванных наций и представляла их жертвами Гитлера. Две крупнейшие ошибки России в ее геополитической политике после войны помогли США быстро ликвидировать успехи России, а затем и поставить ее на колени: Первая ошибка --- административное деление советской зоны, которая контролировалась советскими войсками, по прежнему этническому признаку. Пропагандой коммунистического принципа интернационализма и использованием  прошлого исторического опыта (согласно теории, больше тысячи лет назад русские пришли с берегов Эльбы — вспомни евреев, которые покинули Израиль две тысячи лет назад!)  легко было разделить советскую зону на страны, внутри каждой из которых были бы, по крайней мере, две противоборствющие национальности (поляки и немцы, поляки и словаки, болгары и румыны, сербы и венгры и т.д.) В восточной Германии, в пограничных районах поселить русское население, как в Кенигсберге, и в частности, Берлинскую область заселить русскими, а немцев выселить в Среднюю Азию с гораздо лучшими климатическими  условиями жизни, чем в Германии. Если бы Сталин был на 20 лет моложе, он так и сделал бы. К сожалению, коллективный разум русской нации  контролировался евреями, которым это было невыгодно.       Вторая ошибка --- соревнование коммунизма с капитализмом, которое с восторгом принял богач дядя Сэм. Он немедленно завалил свою Европу деньгами и помощью (план Маршалла). Россия выбивалась из последних сил, ублажая бывших врагов и помогая европейским нациям-сателлитам, чтобы поднять их уровень жизни (который  должен был  быть выше уровня жизни Западной Европы!) и доказать премущество коммунизма над капитализмом, конечно, за счет ухудшения жизни своего народа.  Это — настоящий идиотизм  советской политики того времени, искусно направляемой евреями.  Преимущество коммунизма — морально-этическое, а отнюдь не материальное.

Некоторые русские авторы думают, что достаточно опубликовать свою работу за границей — и успех обепечен. Это верно только тогда, когда у этого русского — еврейская фамилия. Тогда ему, действительно, обеспечена поддержка и цитирование международных евреев, которые доминируют в финансах, политике и, частично в науках, в США и многих других странах, включая Россию. Это—простая констатация фактов. Как сказал главный рабби Калифорнии Rouben :”There are Jews by birth, Jews by choice, and Jews by association”. Таким образом, сами евреи считают, что, например, Молотов, Калинин, Ворошилов, Брежнев, Медведев суть евреи, согласно последней категории. ( Rouben сказал это в связи со вступлением дочери экс-президента Клинтона в брак с евреем.) Поэтому тому, кто мечтает о признании в США (да и не только в США), нужно, прежде всего, доказать свою причастность к евреям по одной из этих категорий (например, поменять фамилию на еврейскую). Мои друзья Леонов и Ушицкий, этнические евреи, жаловались, что их русские фамилии мешали их карьере и им приходилось доказывать свое не-русское происхождение. Такая же история произошла с Ушеренко. Думаю, что лет за 60 евреи разрушат США — главный объект их внимания сегодня. Как? Трудно сказать. Вспомним Россию прошлого века вначале с открытой, а затем - завуалированной, гегемонией евреев. Вспомним историю Древнего Рима, разрушенного христианством евреев-проповедников. Если Россия сможет вырастить немногочисленную научную элиту мирового класса, то она выживет и её ждет счастливое будущее. Мой инвариантный интеграл выведен для динамики любых твердых материалов и сплошных сред (см. статью [9] с его применением в снежных лавинах), а не только для случая статики нелинейно-упругих материалов, рассмотренного Райсом. И, что наиболее существенно, работы Райса[1] и Эшелби[10] не имеют отношения к механике разрушения, так как они не касаются роста трещин — предмета механики разрушения. Работа Райса — по концентрации напряжений, а Эшелби — по физической теории дислокаций. Только четыре года спустя Ландес и Бегли[11] применили J-интеграл ,по существу, переписав, в других обозначениях, мой критерий роста трещин, введенный в [1], без всякого цитирования, как это принято на Западе. В некоторых работах J-интеграл стыдливо называют интегралом Эшелби-Черепанова-Райса.

.

С самого детства на мне лежали тяжелые мужские обязанности (например, заготовка дров — основного источника энергии в деревне). С семи лет я не расставался с топором, ходил в лес или за реку за дровами (кусты, тальник и т.п.), рубил, притаскивал домой на спине или на санках если зимой, снова рубил или пилил, и складывал дрова в порядке в сарай. Снабжение водой, то есть таскание ведер с водой от колодца до дома --- также моя обязанность. И так далее.  Никто меня не просил и не заставлял. Я выучил по нескольким печальным опытам, что если я не сделаю этого своевременно, то все мы умрем без тепла и воды --- точно также как ребенок учит  опытным путем, что огонь жжет, а языку  больно, если им лизнуть морозную железку. А мама всегда была на работе, зарабатывала на хлеб насущный. Все это приучило меня к самостоятельности и независимости. Я привык быть сам начальником.        За это мне также пришлось поплатиться впоследствии. Когда меня периодически выгоняли с работы, поиски новой работы были очень трудным  делом для меня. Я как-то недавно анализировал причины, почему у меня не складывалось хороших отношений с администраторами. Оказалось, нет --- с Галиным, Ершовым и Ильичевым (вице-президент РАН, президент Дальневосточного филиала РАН)  у меня были прекрасные отношения до самого конца и при всех скверных обстоятельствах. Все они — совершенно разные люди. Общее у них было лишь то, что они смотрели на меня снизу вверх. Видимо, умные люди хорошо понимали это. Вспоминаю, мне передали слова Седова, когда кто-то попросил его взять к себе безработного Черепанова: «Чтобы он стал моим начальником? Нет, не могу».         Честный еврей, но не «жид». Я его всегда уважал.         Постоянные драки  были реальностью моего существования с самого детства. В Горьком я попал в воровскую шайку. Научился на ходу зацепляться за кузов грузовика на шоссе, запрыгивать в кузов и ехать без всяких разрешений—или хвататься на ходу за тендер трамвая или буфер железнодорожного вагона и ехать куда- надо без всяких билетов. Учили и воровать, демонстрировали в городском саду, как незаметно вытаскивать что придется, обычно платочек или рубли, у девиц из карманов. Слава богу, мне не пришлось самому вытащить ни копейки, хотя, каюсь, я  молча наблюдал воровство, без протеста и не помогая жертве ( как о том меня учила мама) --- первая стадия морального разложения. Все это происходило  параллельно с Николаем Ивановичем и моим знатным статусом в школе. К счастью, вскоре мы покинули Горький.         Впрочем, некоторыми уменьями я пользовался не раз и много позже. Когда я окончил школу в мае 1954 года, я взял  офицерскую сумку  отца, в которой поместилось только полотенце, носки, тетрадь, медаль и школьные документы, а также горбушку хлеба и несколько вареных яиц (все остальное имущество—на моем теле) и покинул навсегда мамин дом, построенный ее братом четыре года тому назад( мамины  заработки пошли на покупку леса). Я отправился на железнодорожный вокзал, прицепился к вагону на ходу и приехал в Москву без билета. Я знал, что прожить в Москве  на 10 рублей в месяц ( треть семейных месячных доходов), которые мне дала мама, пока я буду сдавать экзамены—очень трудно, надо экономить, а билет стоил несколько рублей. Моя мама, которая не знала о моей бурной жизни,  хотела, чтобы я стал священником, а я еще не знал, чего я хочу, но меня тянуло к математике.

О неприкрытом воровстве моих результатов из моих статей и книг [12,13], опубликованных в лучших издательствах и журналах, можно написать много книг. Не хочу этим заниматься — от этого никакой пользы не будет. Просто хочу предостеречь русских авторов: не гонитесь за славой на Западе, вас обманут и обокрадут — в науке нет законов и правил. Это — мир, где господствуют мафии и национальные инстинкты, где хорошо живется мошенникам и проходимцам. Даже Лобачевскому не помогла его заграничная публикация: Риман и другие математики того времени не цитировали его работу. Только рост и престиж русской математики 20-ого века заставил мир признать его приоритет, однако работа Лобачевского уже не смогла оказать влияние на развитие математики. Фамилии знаменитых русских ученых, даже таких как Ломоносов и Менделеев, малоизвестны за пределами России. А о современных ученых и говорить нечего. Как же быть бедному русскому — начинающему ученому, мечтающему о признании? (Вспоминаю, как Райс и Будянский позабавили меня своим сообщением, что я получил Ленинскую премию за работу[1] — они совершенно не представляли себе российскую действительность!) Ведь академики РАН не очень жалуют своих русских ученых. Например, автор [14] даже не упомянул мою фамилию, излагая мой инвариантный интеграл (называя его, как и многие другие русские авторы, интегралом Райса), правда, « без злого умысла», как он сообщил мне в своем письме, а потому, что «не читал» мою книгу ( с рукописью которой он знакомился 40 лет назад по поручению Новожилова (Пр.5), как мне сказал тогда сам Новожилов). Таким образом, вирус Запада поразил академиков РАН. Поэтому для честного молодого человека ситуация безвыходная. Лучше идти в бизнес, где всё чётко измеряется деньгами, а науку и политику оставить ловкачам.

.

В Москве я отправился на Моховую, в приемную мехмата МГУ, где медалистов принимали без экзаменов, но стипендия маленькая, 29 рублей, как на нее прожить? Прошел по двору, вижу плакат МФТИ: стипендия  45-75 рублей, но медалисты как все сдают экзамены. Проспал на скамейке в каком-то парке и на следующее утро сдал документы в МФТИ. Сдал экзамены в десятке лучших, хотя за месяц опух от голода и покрылся весь чирьями. В моей группе 649 все одиннадцать человек были медалисты, а приняли всего 200 человек из  около 10000 заявлений. Пять человек из группы стали докторами, остальные, кажется, - кандидаты. В общаге МФТИ я впервые познакомился с белой простынью и тогда же увидел первое кино. Мои новые товарищи смеялись надо мной, над моей темнотой, считали, что я "валяю ваньку", так как не верили, что я не знал очевидных вещей, которые знали все. К тому же, я  не был комсомольцем---единственный случай за всю историю физтеха — и не собирался вступать в комсомол. Мама была твердо уверена, что партийные и евреи — нечестные люди и надо держаться от них подальше. Позже в моей жизни оказалось, что это невозможно и что среди евреев и коммунистов немало хороших людей.        Побои также были обычным делом. Последний раз меня пороли, когда я учился в третьем классе — не помню, за что. (После уже справиться не могли.) Дед привязал меня к моей железной кровати ( мы квартировали маленькую комнатушку на троих, а он со сварливой женой занимал другую комнату) и порол меня ремнем. Мама стояла рядом, плакала, а я не плакал — сказывалась деревенская тренировка — кто не может терпеть боль, считался слабаком.  Это здорово помогло мне потом, особенно, последние 40 лет. Если бы я не выносил боли, как все нормальные люди, я бы умер давным-давно, как умерли все мои школьные друзья и многие студенческие друзья-неудачники. А я как свирепый сорняк выжил. В отличие от культурной травы, которая растет, когда ее поливают, сорняк растет просто потому, что не может не расти.       Ректором  физтеха (МФТИ) был, как и ныне, академик Белоцерковский. Деканом был Моисеев, он называл/дразнил меня  «володимирский мужик», о чем я вспоминаю с гордостью. («Мужик» для меня с детства было похвальным словом, а Моисеев не мог понять, почему я улыбаюсь. Мой окский говорок, который, говорят, чувствуется и сейчас, резал слух культурных людей.)  Матанализ читал академик Никольский. Аналитическую геометрию читал академик Делоне. Гидродинамику читал академик Моисеев. Теорию упругости и прочности читал член-корреспондент Соколовский. Теорию оболочек читал академик Векуа. Теорию функций комплексного переменного (ТФКП) читал академик Овсянников. Теорию горения читал академик Ваничев. Конечно, все они, за исключением Соколовского и Векуа, еще не были тогда членами РАН --- их выбрали позже. Я привел этот список, чтобы показать, что такое был физтех тогда --- элитный вуз.

В заключение приведу простейший пример инвариантного интеграла, взятый из книги [13], чтобы показать мой метод и вклад Райса. Стационарное течение идеальной несжимаемой жидкости описывается следующим инвариантным интегралом, который выводится моим методом из закона сохранения энергии- импульса для жидкости, заключенной внутри замкнутой поверхности S Здесь : ρ , p , Vk  и nk -- плотность, давление и компоненты скорости жидкости и орта к поверхности S. Ее можно как угодно деформировать, не пересекая источников и вихрей — значение интеграла не изменится вследствие закона сохранения (инвариантность). Следуя Райсу, применим теорему дивергенции к интегралу в левой части уравнения (1), получим : ( V—область внутри S ) Cогласно локальной формулировке закона сохранения, полученной Эйлером Подставляя (3) в (2), получаем уравнение (1), т.е. доказываем инвариантность интеграла. Когда известен сам интеграл, сделать это доказательство нетрудно. Инвариантные интегралы гравитационного, электромагнитного и теплового полей, газовой динамики и механики твердого тела даны в книге [13] и [15]. Увлечение парапсихологией многих ученых, включая Райса, показано в статье [16].

.

Правда, на лекции я не ходил и знакомился с лекторами только на экзаменах. Почему? Присутствие на лекциях оказалось обременительным для меня и для лекторов, так как я часто не понимал там, где всем было понятно и пытался иногда задавать невпопад вопросы, так как, не понимая, я не мог тупо переписывать и раздражался.   Лекторы, да и студенты, которые обычно всё понимали, естественно не любили мои глупые  вопросы. Поэтому уже с первого курса я перестал ходить на лекции и готовился к экзаменам самостоятельно, по учебникам.          Слава богу, физтех тогда был единствнным вузом в стране, где  студентам  разрешалось непосещение лекций, хотя лекторам это не очень нравилось и они были ко мне особенно «внимательны» на экзаменах. Но завалил я  за  все время лишь один эзамен --- Овсянникову. Правда, пересдал его на отлично. С тех пор, ТФКП (теория функций комплексного переменного) стала моим математическим увлечением. Это — мой «конек». Я считаю Овсянникова моим крестным отцом. Ему недавно «стукнуло» 90.  Жив еще, говорят, Никольский---ему сейчас 105 лет (пример, которому невозможно подражать!). Остальные все — в могиле. Студенческая жизнь --- беспорядочна, как принято вежливо писать. Не буду здесь об этом писать. Сами понимаете, молодо-зелено, кровь бурлит, секс одолевает, и в спорте нельзя никому уступить, а соперничество иногда к добру не приводит. Каждое лето я работал грузчиком на самых тяжелых работах (помню, приходилось таскать на горбу тюки весом 150 кг). Почему грузчиком? Потому что там можно было заработать за месяц больше, чем зарабатывал старший научный сотрудник Академии наук. А деньги нужны были на развлечения, на вино — надо было также помогать маме и младшему брату.       На последнем курсе я познакомился с Христиановичам и Баренблаттом, а также видел много других великих ученых. Королев, Келдыш, Лаврентьев, Ландау и другие  в то время буквально гонялись за выпускниками физтеха, зазывая их к себе в аспирантуру или на работу.  Баренблатт увлек меня своим рассказом  о трещинах, - я решил пойти к нему и его назначили моим рукововодителем по дипломной работе, хотя Соколовский хотел, чтобы я остался на его кафедре, где я делал дипломную работу. Меня отговаривали со всех сторон: один из моих друзей «пошел» к знаменитому Ландау, другой — к знаменитому Капице, а я «пошел» к молодому еврею, который только недавно, в возрасте 30 лет, защитил докторскую диссертацию.

Инвариантные интегралы позволяют вывести единым методом все классические законы физических взаимодействий. См. книги [12, 13, 15, 17], где этим методом выведены известные законы Ньютона, Кулона, Био-Савара, формула Ирвина, формула Пича-Келера в теории дислокаций, формула Жуковского-Чаплыгина подъёмной силы крыла самолёта и многие другие. В качестве примера приведу изящную формулу для силы взаимодействия двух релятивистских зарядов, движущихся вдоль одной и той же прямой где Здесь: F---сила взаимодействия двух зарядов (положительная в случае силы притяжения и отрицательная в случае силы отталкивания), Q1 и Q2 ---- движущиеся электрические заряды ( второй заряд вслед за первым), D--- расстояние между ними в собственной системе координат, V--- скорость движения зарядов, а ---скорость света в среде (материале), которая всегда меньше с, с---скорость света в вакууме, ε --- относительная диэлектрическая постоянная среды, показывающая, во сколько раз сила взаимодействия зарядов в среде меньше, чем в вакууме (ε = 1 в вакууме, а в любой среде ε > 1 ) В частном случае покоящихся зарядов, когда V = 0, будет М = - 1 и формула (4) даёт классический закон Кулона, известный с 18-ого века.

.

Что ж  делать? — я всегда поступал вопреки советам и здравому смыслу. И всю жизнь мне приходится расплачиваться за мои ошибки. Баренблатт сначала посчитал меня деревенским  «долб...бом» и общался очень и очень неохотно,  а после того как я принес ему свою готовую дипломную работу, которую я написал самостоятельно, то есть сам выбрал тему и нашел решение, ни о чем его не спрашивая, он вдруг ухватился за меня и «заласкал любовью». Подробности можно найти в   рассказе Гены Чера «Обман», где все описано документально точно. История — занятная. Советую  прочесть ее. Не буду пересказывать те яркие события.       Итак,  уже через полгода после защиты диплома, к лету 1960 года, я стал его  «правой рукой», как называли меня сотрудники Баренблатта. Объясняю, что это фактически значило. В кабинете Баренблатта в только-что открытом Институте Механики МГУ стояло два стола, за одним сидел он сам, а за другим—справа от него—мой стол. Напротив—большая черная доска с мелками и тряпкой. Около двери — платяной шкаф, напротив двери — большое окно с видом на китайское посольство. Директор института Горемир Горемирович Черный, потомок тех немногочисленных чехов, которые были взяты в плен генералом Брусиловым во время его знаменитого похода в Силезию в 1915 году и которые потом перешли на сторону советской власти, в то время как большинство пленных чехов стали грозной антибольшевистской силой в 1919 году. Он — ученик Седова и друг Баренблатта, с которым вместе учился на мехмате МГУ. Бывший солдат, прошедший всю войну.           Баренблатт сразу запряг меня в работу. Каждое утро я приходил на работу , хотя  никогда—к 9-и часам, как приходил Баренблатт, что вначале его раздражало и он пытался делать мне строгие выговоры, но постепенно привык и смирно ждал моего прихода, так как без меня он все равно не мог делать наши «совместные» работы. Кроме того, он частенько просил меня делать иногда довольно трудные вычисления для его собственых статей. Но большую часть моего времени отнимала работа с его аспирантами. Их было несколько, кроме меня. Все—евреи, для которых у Баренблатта было точное  определение: «еврей-дурак».          Но он так называл их, разумеется, за их спиной и специально для меня —своеобразная «похвала» моим стараниям. Вначале они, входя в кабинет, обращались к Баренблатту,     но он неизменно говорил что-нибудь вроде:  «Обращайтесь к Геннадию Петровичу по всем вопросам, он Вам поможет». Постепенно они перестали обращаться к нему и постоянно по всем научным вопросам имели дело только со мной. Я вначале был страшно горд таким доверием, Баренблатт напоминал мне Николая Ивановича.

Поэтому Евгений Михайлович Лифшиц (Пр.2) назвал формулу (4) при условии (5) формулой Кулона-Борзых-Черепанова и немедленно опубликовал статью [18], где она была впервые получена, в своем "Журнале экспериментальной и теоретической физики"(Пр.6), наиболее престижном российском издании по физике, пользующемся мировой известностью. См. также статью [19], опубликованную несколько позже в ведущем журнале по прикладной физике, где этот закон был использован при анализе аномальных эффектов разрушения твёрдых материалов электронным пучком. Анонимный рецензент этой статьи в Journal of Applied Physics (Пр.7)охарактеризовал этот результат “as a Nobel-caliber result”. Анализ зависимости силы взаимодействия одноимённых зарядов от скорости М (V) показывает, что с увеличением скорости сила отталкивания уменьшается и при скорости, равной скорости света в среде ( когда V = a ), обращается в нуль. Когда скорость движения зарядов становится больше скорости света в среде (т. е. когда V > a), сила взаимодействия одноимённых зарядов становится силой притяжения, которая, однако, действует лишь на второй заряд, движущийся следом за первым. (Передовой заряд находится вне конуса Маха заднего заряда и не подвержен его влиянию.) Эта сила при равновесии всех прочих сил притягивает второй заряд к первому и они слипаются в один заряд. Если поместить третий заряд вслед за вторым, то действующая на него сила притяжения от двух передних зарядов будет ещё больше, что приведёт к слипанию трёх зарядов. В случае цепочки из нескольких зарядов будет иметь место такое же прилипание всех зарядов к переднему. В электронных лучах в таких цепочках образуются кластерные заряды из многих миллиардов электронов, обладающие большой разрушающей силой. Надо иметь в виду, что формула (4) дана в абсолютной электростатической системе единиц СГСЭ, в которой основными единицами являются сантиметр, грамм, секунда, а абсолютная диэлектрическая проницаемость считается безразмерной и равной единице для вакуума. Следует отметить, что реальность сверхсветовых электронов в среде была доказана впервые Черенковым (Пр.3), который наблюдал свечение от волны Маха, возникающей при сверхсветовом движении электрона. Этот эффект носит название эффекта Черенкова-Вавилова и удостоен Нобелевской премииию. (Вавилов (Пр.4) был тогда президентом Академии Наук и помог теоретически объяснить этот эффект.) Г.П.Черепанов 6413 SW 113 Avenue, Miami, Florida, USA genacherepanov@hotmail.com март 2010 года

.

Хорошо помню Маркузона и Партона, которым я делал задачи по их кандидатским  диссертациям  и провел с ними массу времени, объясняя и разжёвывая им свои вычисления, которые они потом защищали в качестве кандидатских диссертаций (правда, после того как я защитил докторскую). С другими я имел лишь эпизодические контакты.  Я не мог понять, зачем Баренблатт их взял в аспирантуру—он не ставил им никаких задач, как мне жаловались оба, а если ставил,  задачи оказывались слишком трудными. И пользы, абсолютно никакой, ему  от них не было.  Потом, узнав ближе Баренблатта, понял глубокую суть его  национально-политической деятельности, столь необычной для русских людей. С любым великим евреем, будь то Зельдович, Ландау, Левич, не говоря уж об университетских математиках, он быстро входил в близкий контакт и пользовался их полным доверием и поддержкой. С русскими великими учеными у него получалось иногда хуже, хотя он был непревзойденным мастером «подлезать». Мне передавали, что Колмогоров, его руководитель по кандидатской диссертации, сказал ему следующее, когда Баренблатт принес ему свою первую работу: «Это — собачье говно! Знаете, почему? Потому что собачье говно не годится даже на удобрения!».             Когда в его кабинет входил иногда академик Работнов, одетый, так как его кабинет был дальше по коридору, Баренблатт вскакивал и, кланяясь, подбегал к академику, чтобы снять с него пальто — как швейцар, чтобы подчеркнуть свою преданность. Обычно я смеялся потом над ним, но он всегда находил оправдание типа: «Он — настоящий великий человек, Геннадий Петрович! Он решил такую трудную проблему!».  И это, действительно, казалось для меня часто своего рода  уважением к научным подвигам академика, а вовсе не элементарным подхалимством. Однако к людям более низкого звания у него не было такого уважения       Особое удивление и, я бы сказал, восторг вызывал Партон, разбитной парень, умница, который знал всё на свете, круглый отличник мехмата, с поразительной памятью, энергией и работоспособностью (от которой он с ранних лет страдал геморроем). Знаток множества анекдотов, которыми он буквально засыпал меня. И при всём том — нулевые творческие способности. С таким парадоксом я потом встречался несколько раз — и только у евреев. Может быть, потому, что тогда мне, в основном, приходилось иметь дело только с евреями.      Надо упомянуть, что Баренблатт еще надеялся использовать неопубликованный класс задач, решение которых мне удалось найти в моей дипломной работе, и он иногда предлагал мне решить и опубликовать (конечно, совместно) некоторые задачи этого класса. Мне с трудом удавалось отбояриться. Ведь, я знал, что это решение неверно (но я не говорил ему об этом, см. рассказ Гены Чера «Обман»). Ему как хищнику мои отнекивания казались естественным желанием «застолбить» за собой этот приоритет, но он был терпелив и крепко держал меня в своих когтях.      Раз в неделю Баренблатт проводил научный семинар, на котором работники других институтов ставили свои доклады. Обстановка была рабочая, неформальная — можно было ставить и обсуждать любые возникавшие вопросы. Я любил эти семинары. Там , еще в 1960 году,  я  познакомился с Борисом Костровым, постоянным участником большинства семинаров. Он работал в отделе Зволинского, в Институте Физики Земли АН СССР.  Должен, наконец, признаться, что, пожалуй, ему больше, чем кому-либо другому,  я обязан открытием инвариантного интеграла, которое я опубликовал впоследствии. Блестящий аналитик и прозорливый ученый,  Костров интуитивно чувствовал этот интеграл и, по существу, использовал его частные случаи  в некоторых  динамических задачах, без всяких специальных подчёркиваний его инвариантности, которая, как я понял  впоследствии, казалась ему элементарным фактом, не заслуживающим особого внимания.

Литература 1.Г.П.Черепанов (1967), ПММ, 31(3), 476-488. 2. J. R.Rice (1968), J.Appl. Mech., 35, 379-386. 3. G.P. Cherepanov (1968), J. Solids&Structures., 4, 811-831. 4. «Мир человека» (2008), 8(4), 151-185. 5. «Вестник СамГУ» (2009), 2(68), 151-185. 6. inc.kursknet.ru/mosdis.htm 7. inc.kursknet.ru/911usae.htm 8. G.P.Cherepanov (Ed.,1998), FRACTURE.A topical encyclopedia, Krieger 9. G.P.Cherepanov, I.E.Esparragoza (2008), J.Glaciology, 54(184), 182-188 10. J.D. Eshelby (1951), Phil. Trans.Roy.Soc., A244, 87-112 11. J.Begley, J.Landes (1972), ASTM STP 514 12. G.P. Cherepanov (1979), Mechanics of Brittle Fracture, McGrawHill, 950p 13. G.P. Cherepanov (1997), Methods of Fracture Mechanics, Kluwer, 320р 14. Н.Ф. Морозов (1984), Математические вопросы теории трещин, Наука 15. Г.П. Черепанов (1987), Механика разрушения горных пород в процессе бурения, Недра, Москва, 305 стр 16. Г.П.Черепанов (2010), Прикл. Механика, 2 17.Г.П.Черепанов (1983), Механика разрушения композиционных материалов, Наука, Москва, 300 стр 18. А. А. Борзых и Г. П. Черепанов (1980), Коллективные релятивистские взаимодействия в электронных пучках, ЖЭТФ, том 78, № 1, 119-122 PDF Ru (американское издание Sov. Phys. JETP, 51(1), pр. 59-69 ) 19. G. P. Cherepanov and A. A. Borzykh (1993), Theory of electron fracture mode in solids, J. Applied Physics, 74 ( 12), pp. 7134-7153. PDF Программа ИНК предоставляет читателям возможности познакомиться в полном объеме с основными публикациями Г.П.Черепанова по инвариантным интегралам в различных средах

.

Кроме того, он был полностью сфокусирован на одной трудной  задаче динамической теории упругости и в то время был чужд всему, кроме этой задачи. Эту задачу я поставил ему на одном из первых семинаров, когда узнал, что он занимается динамическими задачами теории упругости. Я сказал ему: « Я пытался  решить динамическую задачу о движении трещины с переменной скоростью, но пока не смог её решить, однако чувствую, что её решение можно найти. Попробуйте  её сделать.» Конечно, это был мощный стимул для болезненно- честолюбивого и страстного Кострова: «Решить задачу, которую не смог решить даже Черепанов!».            С тех пор, он постоянно занимался этой задачей, рассказывал мне о трудностях ее решения (я сказал ему, что  больше ей не занимаюсь) и, наконец, решил ее через четыре года. Совершенно блестящее решение, которое оставило далеко позади всех заграничных авторитетов, даже самого великого в этой области, американского ученого  Фройнда, который долго, но без успеха, занимался этой проблемой. По моему мнению, Фройнд не составляет и десятой доли Кострова, по творческому таланту. А Фройнд — один из самых почитаемых в США ученых, президент Национального Комитета США по теоретической и прикладной механике. Перед своим докладом этого решения на семинаре, Костров,  как сейчас помню, в красивом ярком свитере,  сказал мне: «Наконец, я ее решил. Я искал это решение далеко, а оно оказалось здесь!» - и он провел рукой по горлу.          Костров — настоящий русский гений, к сожалению, полузабытый и неоцененный.  Он всю жизнь страдал от недостатка внимания к его достижениям. Надо сказать, что дружеских отношений у нас никогда не было и не могло быть, по вполне понятным причинам. Позже он даже критиковал мою работу об инвариантном интеграле, о чем я расскажу далее.         Итак, возвращаясь к «правой руке». Бессовестная эксплуатация продолжалась года полтора, бесплодная работа с тупыми евреями отнимала массу моего времени — ей  не было  видно конца. Когда я почувствовал это, моя гордость испарилась. К этому времени я сделал уже несколько работ, совместных с Баренблаттом. Некоторые из них уже вышли, другие были в печати. Как-то, когда мы были одни в кабинете, каждый занимаясь своим делом, я тихо спросил его:  «Григорий Исаакович, мне уже можно защищаться. Столько работ нет ни у кого, кто защищал кандидатскую в последнее время...»  Он мгновенно ответил, без всяких колебаний, жестко и без обычной милой улыбки:  «Геннадий Петрович, Вы — сильный человек . Вы можете сделать свою собственную работу».          Итак, сомнений не оставалось: он мою работу считал своей и вовсе не собирался даже делиться со мной. Ни о какой помощи с его стороны не могло быть и речи. И любую работу по механике разрушения, которую бы я сделал, мне бы пришлось показывать ему и он бы ее также прикарманил.  Ведь он  же курировал эту область во всех трех журналах по механике в СССР.  Его авторитет был непререкаем. Ситуация у меня была безвыходная. Из его когтей  вырваться было невозможно. Его план стал мне совершенно ясен --- «задушить поцелуем», не давать мне расти, а использовать меня как рабочую, бесправную скотину.  Я был  «правой рукой» для дураков, а на самом деле был бесправным батраком. И жил я на свою аспирантскую  стипендию — даже экономический стимул отсутствовал.

.

"Воспоминания" Г.Черепанова в более удобном формате можно прочитать отдельно по ссылке           Меня охватила паника. Такая перспектива мне не нравилась. Я стал частенько выпивать, благо - жил в общаге аспирантов Академии Наук на Профсоюзной с химиками вместе и чистый спирт был бесплатным. Стал частенько пропускать, вообще, работу за своим правым столом.     Баренблатт заволновался, так как это влияло и на его собственную работу. Он был нетверд в комплексных переменных и в теории упругости и полагался больше на мою экспертизу. Он подарил мне часы, написал письмо моей маме, в котором писал, что я буду великим ученым, и она может гордиться таким сыном. Конечно, она написала мне о том сразу. Когда и это не помогло, он устроил мне психический скандал, говорил, что я — неблагодарен ему (непонятно, за что?). Я понимал, что это — блеф. Мое падение не только как ученого, но просто человека, как личности,  казалось неизбежным.         (Пару раз в тот период, когда он почти махнул рукой на меня, его вонючие аспиранты пытались вызвать меня на безрассудный поступок, очевидно, с его подачи. Помню, как однажды какой-то сосунок сказал мне что-то шутливо-оскорбительное про мою маму и все евреи в комнате, включая Баренблатта, захихикали. Я едва не пришиб тут же жиденка, что было бы концом моей аспирантуры и научной карьеры --- думаю, что только высочайшим кровяным давлением мне удалось сдержать себя. Я  наглядно прочувствовал, что значит  «русский в Израиле»)           Помог совершенно невероятный, анекдотический случай. Однажды Баренблатт шутливо сказал Маркузону: «Вы уже пять лет сидите у меня, давно закончили аспирантуру. Когда работу мне положите на стол? Вот, Геннадий Петрович только второй год в аспирантуре, а уже диссертацию написал.» И довольно засмеялся. Я, не знаю почему, весело сказал Маркузону:  « Да, приходите через неделю, я закончу писанину и покажу диссертацию!» Баренблатт поменялся лицом;  он подумал, что я принесу диссертацию, написанную по нашим совместным работам, что грозило нежелательным обострением наших отношений. Добросовестный, но туповатый Маркузон сказал: «Хорошо, я приду ровно через неделю, в это же время.». А Баренблатт жестко напомнил мне, после того как дверь за Маркузоном закрылась: «Геннадий Петрович, не забудьте наш  договор!»           Уже — договор . Дело серьезное! Впрочем, я уже понял, что по любимой механике разрушения он не даст мне защититься. А я больше ничем не занимался до того дня. Итак — неделя. Я почему-то сразу решил заняться упруго- пластическими задачами. Видимо, сказалось влияние прекрасного человека и ученого Вадима Васильевича Соколовского, который неизменно при каждой встрече спрашивал меня: «Как Ваши дела?» Он хорошо помнил меня по своей кафедре, где я делал диплом и где я решил еще до диплома  одну задачу  по теплопроводности, которую я так и не подготовил для печати, как о том просил меня Соколовский. Я знал, что он прославился точным решением упруго-пластических задач, которые считались тогда самыми трудными в механике.  По причине своего высокого самомнения, я и занялся их решением. Я засел за них и вскоре использовал на них свою любимую ТФКП и краевые задачи.            По-моему, уже на следующий день мне удалось найти решение задачи, которой занимался раньше МакКлинток, известный американский ученый. Решить он ее не смог, а сделал только частный случай этой задачи. Это уже успех, достаточный для кандидатской. Но за пару дней я раскопал целый класс упруго-пластических задач, для которых я разработал метод, основанный на моем решении нелинейной задачи Римана, впоследствии высоко оцененной Гаховым, главным специалистом в мире по проблеме Римана. Короче говоря, через неделю рукопись диссертации была готова и в назначенный час, когда в кабинете были только Баренблатт и Маркузон, я вручил свою рукопись Баренблатту. Его глаза горели еле скрываемым любопытством. Он взял рукопись и начал медленно листать — платок во рту — знак крайнего возбуждения. Я знал, что он ничего не понимает в этом тексте, так как пластичности он не знал вовсе. Поэтому, как я и ожидал, он сказал: «Хорошо, я почитаю ее дома. Позвоните мне как-нибудь через недельку.» А чего звонить — мой стол же рядом с его столом. Это означало, что он будет сидеть на этом чтении до скончания века. Маркузон мне потом так и сказал: «Не думаю, чтобы он быстро прочел Вашу работу».         Но я уже знал, как действовать. Я поставил доклад на семинаре Галина в Институте механики АН  СССР и с большим успехом доложился --- с Галиным там же я и познакомился. Он полюбил меня с самого первого дня и неизменно поддерживал меня впоследствии, в меру своих кротких сил (его звали за спиной «Лев», а иногда, чтобы подчеркнуть его характер «Кроткий Лев»). Замечательный человек и ученый, удивительный брак таланта и скромности, полная противоположность Баренблатту. Две или три  моих  работы были направлены в печать и вскоре вышли. Вскоре — значит три-четыре месяца, скорость, непостижимая для нашего времени. Тогда ученых было мало — все на виду.          Я, конечно, аккуратно рассказывал Баренблатту о своих успехах. Он уже понял, что я его обошел. Но делать было нечего, так как я не задел его интересы. Сердиться не на что, рукопись стала слишком горячей—на ней долго не просидишь. Однажды, месяца через четыре, когда мы сидели рядом и никого в комнате не было, я тихо спросил его: «Григорий Исаакович, мне Лев сказал, что работу можно ставить на защиту. Я выполнил наш договор. Когда Вы дадите добро?»   Он среагировал как умный еврей:  « Геннадий Петрович, нет никаких проблем. Мне Ваша работа понравилась. Ставьте ее на защиту.»      Работу я поставил и успешно защитил на Ученом Совете МГУ. Галин взял меня к себе на работу в Институт механики МГУ, хотя у меня не было московской прописки — это было серьезным нарушением закона. С Баренблаттом мы растались любезно, он всюду называл меня своим учеником, а я по-прежнему посещал его семинары и сохранил своё право обрывать его на его семинарах своими ироническими вопросами, что никому не позволялось. Более того, он снова стал  заманивать на обеды и вел разговоры, пытаясь убедить меня     заняться турбулентностью—самой главной и трудной проблемой механики, по его мнению. При этом он часто повторял: «Теория трещин уже построена. Это — законченная глава механики. Там делать нечего.» Я понял, что он не хочет, чтобы я вернулся к механике разрушения, чувствуя мою тягу к этому предмету. Это было серьезным предупреждением, на его языке, что я не должен соваться в механику разрушения, что я могу заниматься чем угодно, только не механикой разрушения, что он по-прежнему встретит меня в штыки, если я вернусь в эту область.            Опять-таки, к невероятному счастью, в это время, уже в отделе Галина, мне удалось найти точное решение еще нескольких труднейших задач, в том числе, классической упруго-пластической задачи  для пластины с круговым отверстием. Галин бился над ней 20 лет — не мог решить. Я уже писал о реакции Тимошенко и Соколовского. Набралось  много материала высокой пробы в моем портфеле. Галин мне сам как-то сказал: «Геннадий Петрович, Вы можете уже защищать докторскую по своим работам». По-моему, мне еще не было тогда 26 лет. Я, конечно, не растерялся, подготовил диссертацию, подождал, пока выйдут основные статьи в печати и защитился. Баренблатту сказать было нечего, так как механики разрушения не было в моей докторской. Правда, я чуть не пострадал из-за того, что он называл меня всюду своим учеником. Ильюшин ненавидел Баренблатта и немедленно выступил на защите против меня, но его аргументы были аргументами настоящего ученого, по существу. К счастью, мне удалось парировать его вопросы, и он проголосовал «за», публично показав свой бюллетень. Оппонентами были Гахов, Зволинский, Шерман.  (А вскоре,  кандидатские по механике разрушения защитили мои подопечные: Партон и Маркузон.)        После защиты я немедленно приступил к механике разрушения, которая почему-то тянула меня к себе. Думаю, что это было для меня то же самое, что водка — для алкоголика или наркотик — для наркомана. И уже к весне 1965 года я написал основную часть того, что вышло только два года спустя (ПММ, 3, 1967)---чрезвычайно долго по сравнению со всеми моими предыдущими работами. Выведенный интеграл для потока энергии в конец растущей трещины, а точнее ½ его,  я обозначил буквой  γ, первой буквой моего имени, которое греческого происхождения и пишется так:  γ ε n α δ ί  (означает «благородный»).  Вот какой мелкий честолюбец я был тогда!   Инвариантности интеграла, как и Костров, я не придавал никакого значения — она была совершенно очевидной, и контур в первоначальных вариантах статьи был произвольным. См. также замечания к английскому варианту этой статьи в энциклопедии FRACTURE, Krieger, 1997. В работе указано, что трещина не растет, когда интеграл меньше γ, так что моя γ в точности равна  Jc , введенному  в 1971 году Бегли и Ландесом со ссылкой только на Райса, который , вообще, роста трещин не рассматривал.         Передряги, которые мне пришлось пережить перед публикацией этой работы, описаны в моих мемуарах  «О дискуссиях и ученых» и  «Научные сражения: Москва, 1960-ые годы». Поэтому, не буду повторяться, а приведу только некоторые подробности, не упомянутые в тех мемуарах.        Впервые я доложил работу на семинаре Баренблатта весной 1965 года. Без его одобрения я не мог тогда ее опубликовать, в любом случае. Он не сразу понял, в чем дело, но его сразу поразил мой подход тем, что он применялся к любым материалам, а не только хрупким. Помню, Салганик несколько раз выступал и пытался опровергнуть мое доказательство для ЛЮБОГО контура. Сначала он рисовал какие-то сложные спирали с бесконечным числом пересечений радиусом-вектором. Я, чтобы не вдаваться в такие детали, сказал, что рассматриваю только такие контуры, которые любой радиус-вектор пересекает лишь  в одной точке. Потом он выступил снова и привел пример контура, разрывного в каждой точке. Я остановил его, сказав, что рассматриваю только гладкие, дифференцируемые уравнения контура. После этого он успокоился и не знал, как возражать.         Костров все время сидел молча и переживал. Он никогда не занимался пластичностью и вязкоупругостью—тогда это было ново для него. Потом он выступил с критикой и сказал, что этот подход годится лишь для стационарных трещин, растущих с постоянной скоростью. Я ответил, что у меня рассмотрен лишь случай бесконечно-малого контура любой формы, стягивающегося в конец трещины в любой сплошной среде при любой скорости трещины, но, как очевидно из моего метода, в случае поля, стационарного в системе координат, связанной с этим концом, значение моего интеграла  не изменится, если контур расширять и деформировать как угодно в области стационарности. Последнее  выполняется всегда в статических задачах для упругих тел, как линейно, так и нелинейно-упругих.  Упругое поле всегда стационарно в этом случае и, как очевидно из самого метода согласно закону сохранения энергии, мой интеграл сохраняет свое значение при любом расширении и деформации  контура интегрирования. Это мое объяснение  удовлетворило Кострова и он не возражал.         Баренблатт выступил и сказал, что главный результат этой работы— точное автомодельное решение для несжимаемого степенного нелинейно- упругого материала, а механику разрушения публиковать не нужно, поскольку она уже создана в его работах. Другие выступления я не помню — возражений не было.     В этой работе было пять параграфов: 1. Вывод интеграла для произвольного сплошного материала и произвольного контура 2. Вывод из него формулы Ирвина (линейно-упругое тело) 3. Степенное нелинейно-упругое тело (приложение интеграла) 4. Идеальное упруго-пластическое тело (приложение интеграла) 5. Вязкоупругое тело (приложение интеграла) В последнем параграфе допущена неточность, исправленная в книге и последующих публикациях (см. FRACTURE)          Начались мытарства с публикацией работы. Я докладывал ее также на семинаре Галина и  на всесоюзной конференции по трещинам во Львове. Когда я принес статью в ПММ, Николай Андрианович Талицких, который держал в своих руках ПММ и еще два журнала по механике, долго не давал ответа, а потом сказал, что рецензент написал отрицательный отзыв. Я попросил отзыв, он не дает, говорит, я не хочу Вас расстраивать. Стал советовать мне оставить в работе только третий параграф, посвященный несжимаемому, степенному  нелинейно-упругому материалу. Я сразу понял, откуда ветер дует.          Это был колоритный, незаурядный человек, хотя и далекий от науки: в моей статье он вряд ли понимал даже, о чем она — научной степени у него не было. Рождения 1899 года (он хвалился всегда, что родился в прошлом веке), огромный, грузный, мясистый, с низким голосом—олицетворение власти и энергии. Одной ноги не было — ходил всегда с костылем под мышкой. Рассказывали, что он служил офицером в армии Деникина,  ему оторвало ногу «красным» снарядом и он убежал на одной ноге в Америку. В Нью-Йорке работал в порту грузчиком (представляю, на одной ноге!), пока через несколько лет не познакомился с агентом НКВД (видимо, это было после установления дипломатических отношений с США в 1933 году), выполнил какое-то важное задание и вернулся в Россию. Немедленно вступил в партию, познакомился с Кочиным и Галеркиным, и энергично  занялся издательским делом механики, тогда сконцентрированным в одном журнале ПММ. Все академики выросли на его глазах и с его поддержкой. А политик он был хитрый и дальновидный.            Прежний директор Института механики Ильюшин хотел убрать Талицких  из журналов     «по причине некомпетентности в научных вопросах». Передают, что,  узнав о том,  Лаврентьев сказал про Ильюшина:  « Ну, это он против ветра сцит!» Как раз в это время (1965 год) Талицких был одним из главных организаторов нового Института Проблем Механики (вместе с «Шуриком» Ишлинским и «Гришей» Баренблаттом, в одной компании), где возглавлял  отдел. Говорят, он получал з/плату с пяти мест, в сумме больше некоторых академиков. Во всяком случае, он был очень состоятельным человеком, по тогдашним меркам, так как одним из первых купил новую «Волгу». (Главный редактор журнала ПММ, член-корреспондент Галин, не накопил на «Волгу» за всю свою жизнь.) За несколько дней до смерти Талицких в  1971 г.  я встретил его случайно в аллее около метро, недалеко от Института мехники, уже смертельно-больного раком. Задыхающийся, красный от напряжения, с бешеными, налитыми кровью глазами, он шел энергично как танк и с такой силой махал своим костылем, что весь народ шарахался в стороны, боясь попасть под его костыль. Такова была его реакция на смертельную болезнь—бешенство!  Очень сильная личность. Все академики побаивались его.        Я снова поставил работу на доклад на семинаре Баренблатта, под каким-то другим названием. В самом начале сказал, что это—«почти та же работа»,что получила одобрение на одном из прошлых семинаров, но Талицких печатать ее не хочет, требует, чтобы я всё выкинул и оставил только точное решение для степенного упруго-пластического тела ... и при этом посмотрел на Баренблатта.  Он взял в рот платок — намек все поняли. Доклад был очень коротким — Баренблатт вдруг сказал, что ему некогда, и заключил без всякого обсуждения: « Переделайте всё с произвольного на круговой контур и без тензоров. В конце концов, это прикладная работа для инженеров — им вовсе не нужно знать тензоры и дифференциальную геометрию.»          Так я переделал все на круговой контур и убрал тензоры — работа стала казаться значительно проще и мне показалось даже тогда:  «Смотри-ка, Баренблатт дал дельный совет. Теперь уж эта работа и мои вычисления будут понятны всем!» Хитрый еврей  обманет любого русского!  Через несколько лет, когда поднялся разговор о произвольном контуре, об успехе Райса, я пожалел, что сделал тогда это упрощение. Но без него Талицких даже не принял бы работу тогда. А так она лежала в редакционном портфеле ... но именно, только лежала—без  всякого движения, с весны 1966 года. Дальнейшие события, которые привели к выпуску этой статьи в начале мая 1967 года, т.е. через два года, как я ее сделал, -- описаны в моих  мемуарах «О дискуссиях и ученых» и «Научные сражения: Москва, 1960-ые годы».  Не буду повторяться. Статья вышла исключительно благодаря Льву, с которым мне пришлось немало поработать, чтобы он отважился  пойти против Шурика и Гриши. Шурик не простил ему этого и старательно заваливал потом Льва на выборах в академики.   Как видите, научная работа —  грязное политическое дело.      Следует отметить, что в самом начале моей статьи  говорилось о  контуре  вокруг конца трещины так : «контур С   БЕЗ ОГРАНИЧЕНИЯ ОБЩНОСТИ считается круговым». То есть, хотя вывод дан для кругового контура, он верен для любого. Все, кто знакомились тогда с этой статьей, так это и понимали (как в ТФКП, без дополнительных упоминаний).      С осени 1966 года, то есть за полгода до публикации статьи, я начал работать над книгой по механике разрушения, которую закончил в 1969 году. Как сейчас помню, осенью 1969 года я привез кожаную сумку с законченной рукописью книги Седову в Институт механики МГУ.  Вошел в его кабинет и сказал:  «Леонид Иванович, вот моя книга по механике разрушения. Я ее закончил.» Он знал уже давно, что  я пишу книгу, и   при встречах спрашивал:  «Ну, как Ваша книга?»  и знал даже о многих подробностях (наверное, от Партона, который у него не вылезал из кабинета, видимо рассказывая анекдоты, а также был постоянным слушателем моих лекций по механике разрушения в МГУ, которые аккуратно записывал). Он взял мою сумку с книгой за ручку и охнул:  « Ох, я до дома ее не донесу!» От института до высотки МГУ, где была его квартира, он ходил всегда пешком (расстояние около 800м). Я сказал:  «Ну, давайте, я Вам помогу». Он ответил: «Ладно, я Партона попрошу.» Рукопись книги называлась первоначально «Механика разрушения», но Седов впоследствии потребовал называть ее «Механика хрупкого разрушения». Я не стал спорить.        Теперь необходимо объяснить, почему я начал работать над книгой и что это была за работа. Ведь у меня даже публикаций не было по механике разрушения, хотя материалов накопилось много в результате тайных занятий.  Я уже представлял себе примерно, какая страшная борьба за их публикацию предстоит с Баренблаттом + Талицких + Ишлинский + еврейство. Даже если мне удастся опубликовать статью с интегралом, все другие работы встретят жуткое сопротивление. Поэтому я вынужден был писать эту книгу, чтобы сохранить сделанную работу. Я теперь не имел роскоши на статьи, как прежде. Райс никогда не цитировал мою книгу, хотя он имеет и русский, и английский вариант в своей библиотеке. А в книге -- масса материалов по инвариантным интегралам (некоторые перекрывают  результаты, опубликованные впоследствии многими другими учеными), но нигде неопубликованных кроме этой книги.         Статью иногда цитируют, а книгу, написанную почти одновременно – нет, хотя в ней исправляются некоторые неточности статьи и дается фантастическое количество разных приложений инвариантного интеграла. Книгу никто не искажал — это мой продукт, а статья — продукт насильственный. Когда она лежала у Талицких, я не мог ничего менять --- он бы немедленно отдал мне  статью, и тогда «мочало вертись сначала».             Думаю, что в нормальных условиях я бы опубликовал просто много статей именно по механике разрушения и, вряд ли, стал бы писать книгу. Большую часть  книги пришлось писать, как большую статью, по неопубликованным материалам. Кроме того, я сильно переоценил благожелательное отношение Седова, как понял вскоре по написании книги. Я был нужен ему как борец против Ишлинского, а вовсе не как автор. Сложный, не по моему уму, человек.  План Седова был: Черный — директор Института механики МГУ, а Седов—директор Института механики АН, т.е. взять в свои руки всю механику, а только-что избранный академик  Ишлинский его обошел.          Несколько слов о других событиях 1965-1967 годов. Баренблатт распространял сведения о моих неопубликованных результатах всем, кому мог — и, конечно, не упоминал автора этих результатов.  Например, результат  третьего параграфа моей статьи об автомодельном решении для несжимаемого степенного нелинейно-упругого материала он сообщил своему другу Будянскому. Уравнения для такого материала—весьма сложны и заметить, что именно при коэффициенте Пуассона, равном ½, имеет место автомодельность—нелегко. А после того как это знаешь, дальше решать легко. Кроме того, при помощи своего интеграла я нашел показатель автомодельности — особенность в вершине трещины. Впоследствии,  результаты моего 3-его параграфа стали называть HRR approach (метод Хатчинсона-Райса-Розенгрена, которые годом позже опубликовали свои решения этой задачи, подтвердив все мои результаты, но не сославшись на мою статью)        В 1990 году я спросил Хатчинсона: « Джон, как ты узнал, что решение автомодельно?» (В английском нет обращения «Вы»)  Он сказал:  « В конце декабря 1966 года я отправлялся на стажировку в Англию и Будянский, мой руководитель, сказал мне «Давай займись этой задачей там, она -- автомодельна»» Потом я спросил Будянского: « Берни, как ты нашел автомодельность?» Берни ответил:  «А мне Баренблатт сказал» В то время я работал с ними в Гарварде на деньги из грантов Будянского, Райса и Хатчинсона (они скинулись). Как-только Баренблатт  узнал о том, он немедленно приехал из Москвы в Бостон и жил там несколько месяцев. Каждый день приставал к  Будянскому с телефонными разговорами, хотел, чтобы его тоже пригласили в Гарвард.  «Как завистливый ребенок», сказал Будянский и добавил : «Каждый вечер звонит и долго разговаривает, не дает мне спать.»  Я сказал ему что-то вроде: «Ну, останови его, скажи что-нибудь!»  Берни сказал :  «Да что ты, он знает даже папу римского!» Даже Америка боялась вляпаться в Баренблатта! Берни — добродушный, огромный американец, из его кабинета всегда воняло сигарами на весь коридор. Я этот запах хорошо знал, так как сам курил кубинские сигары несколько лет. Я ему сказал как-то:  « Берни, ты же русский! У тебя русская фамилия, от слова «будить»! Он засмеялся, сказал:  «Знаю. Но я---американец!» Так мне и не ответил. Фамилии Rice, Sanders, Hutchinson—типично американские. Например, в Майами живет не менее ста человек с каждой из этих фамилией. В Citation Index я только недавно обнаружил, что под одной и той же фамилией James R. Rice , на самом деле, работают четыре разных ученых, близкие по специальности—на один и тот же citation index ! Райс—чрезвычайно симпатичный парень, в молодости играл в бейсбол (американская лапта) — самая популярная игра в США. Она требует быстроты и сноровки. Поразительной работоспособности и любви к науке, исключительно общителен и радушен ко всем, кого я знаю, отлично ладит со всеми и никого никогда не критикует. А о таланте исследователя нечего и говорить. Его все любят. Вот уже 50 лет перед ним открыты все дороги Америки, которая поддерживает его во всем:  в финансах, сколько он захочет, в аспирантах и вспомогательном персонале, сколько он захочет, в славе и признании, сколько он захочет. Райс—настоящий, самый популярный гений Америки. Он объехал весь мир,  и даже Сибирь он знает лучше меня.  Женат второй раз. Его жена Рената Дмовска, он привез ее из Польши, в 1980 году, занимается геофизикой, бывшая аспирантка Кострова. Оба — дружелюбные, интересные люди и работают вместе в Гарварде, Рената—в группе Райса. Счастливая пара, счастливая жизнь. Надо сказать, что по человеческим качествам лучшего американца, чем Райс, я не встречал. Поэтому мне очень трудно соперничать с ним, не хочется его обижать, хочется сохранить хорошие отношения и т.д., а между тем, научная борьба всегда приводит к порче отношений и к драке.        Другого выхода нет. В борьбе за приоритет, как в борьбе за власть, только один может быь первым. И в этой борьбе, к сожалению, нет правил!  Казалось бы, просто — кто первым опубликовал, тот и выиграл приоритет. В жизни редко так бывает. Ведь судьями являются множество ученых --- научная публика. А они чрезвычайно редко бывают объективны. Весьма часто оказывается, что национальная поддержка, личные контакты, связь с влиятельными людьми, человеческие качества и тому подобные обстоятельства гораздо важнее времени публикации. В моем споре за приоритет все эти обстоятельства—на стороне Райса. Даже по человеческим качествам он намного превосходит меня, человека угрюмого, необщительного, дикого. Меня до сих пор смущают некоторые события.  Первое—Райс сказал, что он в то время изучал русский язык, чтобы читать мои русские статьи.  Второе — журнал ПММ доставлялся тогда в библитеки ведущих университов США, в частности, Браунского университета, где тогда работал Райс, в течение нескольких дней после выпуска и, значит, моя статья была в университете Брауна уже в начале мая 1967 года. Третье — Райс сдал свою статью в печать в июле 1967 года, а написать ее, зная мой интеграл, для ученого такой квалификации как Райс, можно за три дня. Четвертое — мой интеграл появляется в самом  начале статьи Райса эвристически, без всякой ссылки на первоисточник. Пятое—в 1990 году в Гарварде я спросил его:  «Джим, как ты нашел этот интеграл?» Джим ответил: « Как и ты — из закона сохранения энергии!» Следующий вопрос, который я хотел ему задать:  «А почему же ты не написал этот вывод?»  Но я не задал ему этот вопрос, так как честному Райсу пришлось бы врать, а наши отношения были бы испорчены навсегда. Ответ на мой вопрос очевиден. Приводя это мое доказательство, ему пришлось бы давать ссылку на мою статью, без чего   не избежать обвинения в плагиате, и так или иначе навсегда потерять   приоритет. Единственно возможное заключение --- Райс списал мой интеграл и применил его к более узкому классу задач о концентрации напряжений в нелинейно-упругих телах (1-ый и 3-ий параграфы моей работы). Думаю, что первоначально он не придавал особого значения этой работе. Успех этой работы среди соотечественников и российских русофобов был для него неожиданным.          Как ведет себя Райс в данной ситуации?  Как чрезвычайно благородный человек. Он иногда даже милостиво признает, что Черепанов получил инвариантный интеграл механики разрушения  «почти одновременно и независимо». Как настоящий Наполеон, завоеватель научного мира. Правда, своим многочисленным докторантам  непозволительно это делать, так что ни один из более чем ста выпущенных им докторов ни разу не признал приоритет Черепанова. Я однажды прямо спросил Райса: «Джим, ты признал мой приоритет в письмах и в личных беседах не отрицаешь этого, а почему ты никогда не цитируешь мои работы, которые ты хорошо знаешь, как я убедился?» Джим тотчас откопал где-то пару своих статей с сылками на мою статью и сказал абсолютно честно, прямо глядя мне в глаза: « Генади, ты не прав! Я очень аккуратно цитирую тебя.» Я подумал, что может быть, действительно, Райс здесь не при чем, а просто его подталкивают соотечественники. Кто же откажется от лишнего куска славы! Просто англо-американская нация — очень  дружная и дисциплинированная, в отличие от российской. Как-то я прочел историю про одного американского прокурора, славившегося своей честностью и благородством. За всю свою жизнь он не совершил ни одного нечестного поступка (одно время я называл Райса  непорочной девой Марией, он был очень доволен). Потом оказалось, что один нечестный поступок прокурор всё-таки совершил:  в молодости, будучи заместителем прокурора, убил его, чтобы занять его место. Райс напоминает мне этого прокурора. О Сандерсе. Я не читал его статью просто потому, что не знал тогда английского языка. Впоследствии кто-то, кажется Ивлев или Рыбаков, показали мне ее. Насколько  помню, у Сандерса—линейно-упругое тело с полубесконечным разрезом, круговой контур на бесконечности. Если моя статья может с ним пересекаться, то только своим  коротким, на полстраницы, 2-ым параграфом, где рассматривается приложение моего инвариантного интеграла механики разрушения сплошных сред из 1-ого параграфа—к линейно-упругим телам. Однако, насколько я помню, у Сандерса нет основного результата моего параграфа—формулы Ирвина, которую Ирвин вывел ранее другим методом. А если из Сандерса вытекает инвариантный интеграл даже только для линейно-упругого тела, то у Райса возникает серьезная этическая проблема, поскольку он, конечно, знал статью Сандерса, но не цитировал ее в своей статье 1968 года. А инвариантность моего интеграла используется чуть позже, но до выхода статьи Райса, в других моих статьях и книге,  в частности,  в обзорной статье,  опубликованной   в  1968 году   в J. Solids and Structures. (эти публикации замалчиваются, создавая впечатление для публики, что статья 1967 года—моя единственная, посвященная инвариантным интегралам).       В 4-ом параграфе с идеальным упруго-пластическим телом  вычисление дало  точный результат: мой интеграл равен нулю! (Правда, я в пол-шаге остановился, чтобы не вызывать огонь на себя,  и опубликовал результат вычисления в последующей работе в J. Solids& Structures, 4(4), 828, 1968, которую я написал по специальному приглашению из этого журнала, а иначе мне не разрешили бы ее посылать по своей инициативе).     Я интерпретировал этот результат НЕВЕРНО —что трещина не может расти в таких материалах. Правильная интерпретация—трещина начинает расти уже при бесконечно-малой нагрузке! Я  вскоре после публикации обнаружил эту ошибку, но нигде не говорил о ней, так как никто ее не заметил, а я долго не мог понять этого парадокса, пока не сделал наномеханику разрушения  20  лет спустя  и не вычислил критический коэффициент интенсивности в кубическом кристалле с трещиной, при котором первая дислокация вылетает из  конца трещины и садится на некотором расстоянии от него, так что трещина передвигается на величину межатомного расстояния (начало роста трещины). Этот коэффициент оказался в тысячу раз меньше вязкости разрушения (см. обобщающую статью в J. Applied Physics, 78(10), 6249-6264, 1995), т.е. близок к нулю!          Кстати, эмиссия дислокаций, которая привела меня к наномеханике разрушения—это вторая крупная работа, где я превзошел Райса. Он работал над этой проблемой много лет, но моя наномеханика разрушения перекрыла все его результаты. Он признал это, когда я предложил организовать дискуссию по проблеме эмиссии дислокаций, а он отказался от дискуссии и просто ушел из этой области молча.  Если бы не моя работа, он бы получил массу премий за свои статьи по эмиссии дислокаций. А сейчас он даже упоминать их не хочет.  Поскольку моя статья была опубликована в J. Applied Physics, украсть что-нибудь было невозможно. А наномеханика разрушения—гораздо более тонкая и сильная работа, чем все инвариантные интегралы. Когда-нибудь, вероятно, уже после моей смерти, она засветится!         Надо сказать, что из источников, цитируемых в работе, я читал в то время (1965 год) лишь Соколовского, Качанова и только-что появившийся перевод книги Боли и Вайнера. Всю литературу на английском, включая две цитируемые статьи Ирвина, я не читал, так как не знал еще английского тогда. Я просто переписал их из обзоров Баренблатта, который всегда отменно знал литературу. И формула Ирвина, которую я кратко вывел во 2-ом параграфе, была взята оттуда же (я тогда боялся, что он вывел ее таким же способом и был очень краток). Я даже не знал тогда американского обозначения коэффициента интенсивности и пользовался обозначением Баренблатта, N. Вообще, все знали, что я — темный человек в литературе. Это верно и сейчас. Честно говоря, не люблю копаться в чужих работах — обязательно обнаружишь грубые ошибки, а от этого - только расстройство нервной системы, отвлечение мозгов и вероятные склоки в будущем. Статья Ирвина, первое, что я прочел на английском, была прочитана мной год спустя (т.е. в начале 1966 года, см. «О дискуссиях и ученых»). Что можно заключить по поводу событий, описанных здесь и в заметке «К истории инвариантного интеграла»? Конечно, все это — печально для меня, автора этого открытия. Представь себе, что ты — крестьянин и в твоем поле орудуют хулиганы.  Или представь, что твою машину угнал какой-то нахал.  Это — то, что происходило и происходит с научными открытиями, денно и нощно. Кто эти нахалы, в данном конкретном случае?  Как очевидно вытекает из этих событий,  отнюдь не Райс,  который служит великой американской нации, а некоторые ученые- россияне, включая академиков РАН, — невольные или сознательные  вши  на беспомощном теле России. Это — пятая колонна врагов России.           А в конечном итоге, все это — гораздо более печально для российской нации. Посмотрите, чьи открытия и приоритеты были признаны. Почти исключительно представителями великих наций и бывших или настоящих супердержав. Слабые нации и государства сдаются и уступают приоритеты своих представителей. Последние сотни лет разгорелась настоящая мировая война наций за открытия и приоритеты. Почему?  Потому что политический престиж и уважение какой-то нации в наше время определяется уже не военными успехами и не территориальными захватами, а научными открытиями, изобретениями и приоритетами представителей этой нации. Ученые в наше время — бойцы и солдаты на своих фронтах в этой жестокой мировой войне без правил. И жертвами этой войны являются слабые нации и государства. Все выгоды и преимущества—более сильным и умным нациям. Это — вечный закон жизни.   Г.П. Черепанов, октябрь 2009 - март 2010 "Воспоминания Г.П. Черепанова" в более удобном формате и с примечаниями можно прочитать отдельно по ссылке