This page:RussianEnglish Disability |
"Информация Наука Культура" - |

|
Открытый Форум 'Социум Экономика Право' Форум о математике |
Г. В. КОЛОСОВ — РУССКИЙ ПЕРВОПРОХОДЕЦ
Gury V. Kolosov, a Russian Who Was the First
Этот очерк представлен автором для первой публикации на страницах програмы ИНК.
Вы можете в режиме он-лайн дискуссии на форуме представить свои мнения о настоящем рассказе, а также оставить комментарии для публикации на настоящей странице.
Некоторые прошедшие события, фамилии и названия, которые упоминаются в рассказе, требуют примечаний для современного читателя - некоторые из них даны сайчас в конце очерка по интерактивным сноскам, мы надеемся что автор, наша програма и сами читатели будут их дополнять.
Г. В. КОЛОСОВ — РУССКИЙ ПЕРВОПРОХОДЕЦГ. П. Черепанов (Пр.1)
| .< |
|
В чем существо достижения Колосова? Теория упругости является главным разделом курсов механики материалов и механики разрушения, которые читаются в тысяче американских университетов и сотнях других университетов в мире. В России курс механики материалов, носящий название сопромата, был высмеян пасквилянтами и стал редкостью в российских университетах. Знание механики материалов совершенно необходимо для изучения более сложного математически курса механики разрушения. Без скрупулезного знания механики материалов и механики разрушения сегодня нельзя создать конструкцию, машину или строение, отвечающие современным потребностям человека. Теория упругости, созданная в 18-ом и 19-ом веках трудами Эйлера, Коши, Сен-Венана и других западных ученых, приводит к необходимости решения сложных математических проблем для дифференциальных уравнений в частных производных. Между тем, в 1851 году немецкий ученый Бернард Риман создал общую теорию функций комплексного переменного, открывающую возможность эффективного решения множества проблем, формулируемых в комплексных переменных. Это—тот самый Риман, который создал Риманову геометрию, Риманово пространство, Риманову метрику, Риманову кривизну и т.д., которыми мы все пользуемся сегодня. Это он первым предложил, что мы живем отнюдь не в Эвклидовом пространстве, описываемом теоремой Пифагора, а в Римановом пространстве,--и указал астрофизикам, как определить его кривизну. (Только теперь мы знаем, что, действительно, наша вселенная—Риманово, а не Эвклидово пространство, но еще не знаем достоверно даже знак его кривизны ). Пространство Минковского и теория относительности, т.е. ядерная энергия, ядерная и атомная бомба и т.п., были бы невозможны без Римановой геометрии. Работа Колосова связала важные практические проблемы механики материалов с мощным математическим аппаратом теории функций комплексного переменного, позволившим найти эффективные решения практических проблем. На военном языке, если сравнить проблему с неприступной крепостью, а ученых—с воинами, штурмующими крепости, формулы Колосова—это тяжелая пушка или орудие, которое позволило взять приступом много крепостей. Работа Колосова опередила западную науку на 50 лет—почти беспрецедентный случай в российской практике! Ведь научные открытия делаются обычно более или менее одновременно сразу несколькими учеными. Открытия как-бы «вызревают» в результате предшествующей научной деятельности многих, так что первооткрывателями оказываются обычно более расторопные счастливцы. Первопроходцы, которые в одиночку идут далеко впереди и пролагают путь другим, встречаются редко. Впрочем, не следует думать, что выдающаяся работа Колосова привела к созданию или усовершенствованию каких-то российских машин или сооружений, создание которых требует передовых знаний десятков различных дисциплин. Прорыв лишь в одном направлении недостаточен для прогресса в целом. Например, решение всех проблем с печенью не позволит удлинить жизнь, если не будут решены на таком же уровне проблемы сердца, легких, почек, желудка и т.д.—то, что представляет любую современную конструкцию. |
|
Формулы Колосова использовались в тысячах статей и книг впоследствии. Они сделали имя Колосова, пожалуй, самым известным русским ученым 20-ого века, опередившим такие имена как Жуковский, Чаплыгин, Седов, Капица, Семенов, Ландау, Колмогоров, Соболев. Имя Колосова упоминается обычно без всякого цитирования его работы—знак высшего признания как классика науки. (Впрочем, средства массовой информации не уделяют Колосову никакого внимания, заслуживая быть названными средствами массовой дезинформации.) История этого исключительного признания поучительна и заслуживает некоторого анализа. Прежде всего, каким образом эта работа в трудах российского университета могла привлечь чье-то внимание? Это, по существу, самиздат, то есть нерецензированная и неоцененная работа. В наш век расцвета самиздата, когда каждый может опубликовать все, что ему угодно, в Интернете, важно понять причины успеха публикации такого рода.
|  |
|
В США при оценке рэйтинга ученого, важного при приеме на работу, повышении в должности и т.п. — десять-двадцать статей в трудах конференций или трудах университетов приравниваются одной публикации в рецензируемом журнале. По публикациям в трудах конференций и университетов нельзя даже защитить диссертацию в приличном университете. А самиздатовские публикации в интернете, вообще, не принимаются во внимание. В России рэйтинг ученого определяют числом ЛЮБЫХ публикаций—что есть рай для научных мошенников и ад—для честных, добросовестных ученых. Это—поле, заросшее сорняками, в котором не видно колосьев. Поэтому хорошее и даже выдающееся произведение, такое как работа Г.В.Колосова, почти не имеет шансов получить признание, если оно опубликовано не в профессиональных журналах, без рецензий. Такая история уже произошла ранее с Николаем Ивановичем Лобачевским, который опубликовал несколько статей по неэвклидовой геометрии в Трудах Казанского университета, ничего не зная об одновременных публикациях венгра Боляйи и работе немца Гаусса. Впрочем, о последней мог рассказать ему его учитель немец Бартельс, постоянно переписывающийся со своим прежним студентом Гауссом. (Бартельс—учитель Гаусса и Лобачевского). Конечно же, никто из профессионалов не читал статей Лобачевского. В России таких профессионалов просто не нашлось—Лобачевский был осмеян и умер, не получив никакого признания, так что его работа не оказала никакого влияния на развитие науки. Некоторые считают признанием его работу ректором Казанского университета, но это является признанием лишь его административной, а не научной деятельности: ведь Лобачевский не был даже избран в Российскую Академию Наук, что есть минимально-необходимая мера признания ! К тому же, в то время главной фигурой был попечитель университета, а не ректор, который в любой момент мог лишиться работы по прихоти попечителя.. Только после того, как Лобачевский опубликовал свою геометрию на немецком языке—тогда наряду с французским, господствующем в математике—она стала известной Гауссу, который поддержал ее благодаря имени Бартельса, и Лобачевский получил некоторое признание в Германии, хотя Риман и другие математики никогда не ссылались на его работу. Имя Лобачевского стало известным только в 20-ом веке в связи с подъемом общего уровня и влияния русской математики в мире и под давлением влиятельных русских математиков. Таким образом, в конечном успехе признания имени Лобачевского — три важных фактора: профессиональная публикация, поддержка Гаусса и высокий престиж русской математики в 20-ом веке. Если бы не было этих обстоятельств, клянусь, никто бы не знал фамилию Лобачевского, а русские историки, раскопав его работу, в лучшем случае, говорили бы о талантливом русском ученом-самоучке. Думаю, если покопаться в многочисленных плохо-опубликованных трудах российских ученых прошлого, то можно найти немало настоящих, совершенно неизвестных, бриллиантов—гениальных работ, которые могли бы оказать влияние на развитие науки, если бы были опубликованы в профессиональных журналах. Наши Ломоносов и Менделеев — ныне самые известные русские ученые 18-ого и 19-ого веков, хотя и непризнанные в России при жизни—в молодости проработали по нескольку лет в западных университетах, командированные из России. У Лобачевского и Колосова такой возможности не представилось. |  |
|
Ученый обязан работать не под себя, не только для собственного удовольствия, а для людей—на публику, т.е. публиковать свои труды, если он их ценит, в профессиональных журналах. Иначе, польза от таких трудов, даже если они гениальные, равна нулю. Рэйтинг ученого определяется его профессиональными публикациями в рецензируемых журналах, а не печатными работами . Лет 15 тому назад моя точка зрения по этому вопросу была не такой радикальной, пока один мой американский знакомый не опубликовал—на спор —около 150 статей в трудах конференций всего за один год! Колосов оказался удачливее Лобачевского. Его работу прочел один читатель—профессионал, который оценил ее достоинства и оказался честным и благородным человеком. Это был Николай Иванович Мусхелишвили, энергичный и влиятельный ученый, который сделал блистательную научную карьеру на формулах Колосова, но никогда не умалял их значения. (Последнее не так уж редко встречается: Ньютон, зная calculus Лейбница, никогда его не цитировал; Эшелби, строивший свою работу на работе Максвелла, никогда ее не цитировал; Эйнштейн, воспитанный на работах Римана, никогда его не цитировал, и т.д.) Поэтому Колосов в конце жизни получил некоторое признание, а примерно 50 лет тому назад, когда перевод книги Мусхелишвили был опубликован за границей, начался феноменальный успех имени Колосова. Но фигура Мусхелишвили (Пр.2) с его популярностью и толстой книгой как-то заслонила скромного Колосова. Кроме того, редактора научных журналов из политических соображений стали «помогать» Мусхелишвили, занимавшему высокие административные позиции. Помню, как Н.А.Талицких, редактор всех советских журналов по механике в 1960-ые годы, заставлял меня заменять Колосова на Колосова-Мусхелишвили. (Сам Николай Иванович всегда называл их формулами Колосова.) Как ни велики заслуги Мусхелишвили в популяризации формул Колосова, они должны называться именем первопроходца. Не стоит отказываться от этой древней традиции человечества. Ведь первая публикация студента Мусхелишвили (в 1915 году), совместная с его профессором Колосовым, была основана на формулах Колосова. Она и определила, в основном, будущую научную карьеру Н.И.Мусхелишвили Конечно, даже публикация в самом престижном журнале не гарантирует успеха публикации, хотя и значительно улучшает шансы. Борьба за публичное признание научных трудов—важная и весьма ответственная часть жизни ученого, впрочем не всегда успешная даже у общепризнанных и весьма честолюбивых гениев. |  |
|
Лейбниц опубликовал свое исчисление, которое мы все используем под названием интегрального и дифференциального исчисления, на двадцать лет раньше Ньютона, и даже с комментарием последнего. (Тем более, что исчисление флаксонов Ньютона никто и никогда не использовал, даже сам Ньютон.) Однако Лейбниц умер, всеми забытый и заплеванный, как простой, никому неизвестный мещанин : честолюбивый Ньютон, обладавший неограниченной финансовой и научной властью в самом мощном государстве мира в то время, просто затравил когда-то жизнерадостного Лейбница. В похоронах Лейбница принял участие только один человек—его секретарь. А первый некролог на Лейбница появился только через 50 лет после его смерти. До того ни один редактор не решился на такое. Несмотря на то, что Лейбниц основал Берлинскую Академию Наук и был в течение более 40 лет членом как Французской, так и Британской Академий Наук! Настоящая научная деятельность — весьма опасное занятие. Это, по существу — вечная война с противниками разного рода, и преждевременная смерть — ее обычный результат. Верю в то, что правда восторжествует и , в конце концов, ученые признают «закон всемирного тяготения Гука», а не Ньютона, «модуль Эйлера», а не Юнга, «интегральное и дифференциальное исчисление Лейбница», а не Ньютона, « закон упругости Эйлера», а не Гука, «классическая механика Галилея-Ньютона-Лейбница», а не одного Ньютона, несмотря на Principia c его 26 препозициями (аксиомами) мироздания, которые прочитали только три человека за 300 лет. Неправильно, когда лавры первопроходцев достаются сановитым популяризаторам и «доказывателям»! Еще в 1676 году, через несколько лет после того как Гук опубликовал закон всемирного тяготения, Ньютон не понимал его, так как в своем письме Гуку писал, что тело, притягиваясь к другому, будет приближаться к нему «по спирали», а Гук поправил его, ответив, что «малое тело будет двигаться по эллипсу вокруг большого тела», после чего Ньютон занялся, с большим успехом, эллиптическими орбитами. О «механике Лейбница» имеет смысл напомнить ввиду ее простоты. Лейбниц считал, что движение любого тела определяется его «силой»
Е, которая складывается из «живой силы» 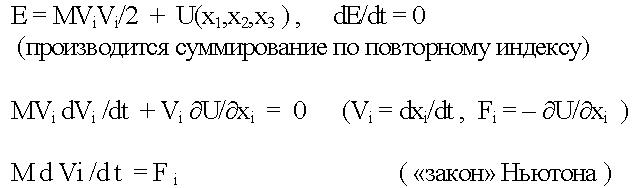 |  |
|
Этот метод Лейбница, применимый только к консервативным системам, был значительно усовершенствован Лагранжем и Гамильтоном впоследствии. (Условие dE/dt = 0 означает закон сохранения энергии в консервативной системе.) При движении вдоль прямой с одной компонентой скорости V механика Лейбница еще проще (что вполне доступно для средней школы, где знакомят с началами дифференциального исчисления): 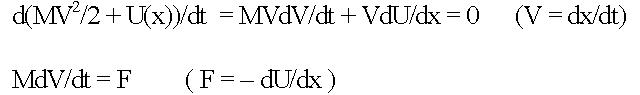 Это уже было до Principia Ньютона, но Ньютон не хотел, видимо, принципиально, использовать известное ему дифференциальное и интегральное исчисление Лейбница и выдвинул свои «законы»--аксиомы, заменив собой бога, как сделал ранее Эвклид. В пренебрежительном отношении Ньютона к Лейбницу, видимо, сказалось и славянское происхождение последнего. Философский конфликт между искренно-верующим оптимистом Лейбницем и «скрытым атеистом» Ньютоном закончился убедительной победой последнего. Несмотря на то, что Ньютон написал больше богословских сочинений, чем научных, никто до сих пор не знает, какую же веру исповедовал Ньютон. В эпоху победы над многими силами природы «аксиоматический» подход Ньютона ( «Это верно, потому что это верно всегда») импонировал людям гораздо больше, чем богословский подход Лейбница («Бог всегда выбирает из всех возможностей наилучшую»). Только в 20-ом веке оказалось, что «законы» Ньютона, в том числе, закон гравитации—чисто-эмпирические (как и считал, по существу, Лейбниц). Тем не менее, до сих пор везде и всюду студентов заставляют зубрить «законы» Ньютона, как некие откровения «чистого разума» гения . Это является явным анахронизмом, который наносит большой вред, так как искажает правильный метод научного познания «от опыта к теории» и ставит «телегу впереди лошади». Этот метод Ньютона нанес непоправимый ущерб сознанию именно русских людей с их верой в чудодейственную силу человеческого разума, в гениев разного рода и в чудо-теории. (По этой же причине теория марксизма стала необычайно популярной именно в России. По той же причине Россия—идеальное пастбище для научных шарлатанов и мошенников. ) Закон всемирного тяготения и законы Ньютона являются эмпирическими законами подобно законам упругости, пластичности, гидродинамики. Они имеют определенные области применения, за пределами которых они—неверны. Так они и должны преподаваться всюду—как ЭМПИРИЧЕСКИЕ ЗАКОНЫ--чтобы воспитать у молодых людей правильный приоритет опыта над теорией, даже самой совершенной. Тогда шарлатанам будет значительно труднее работать.
|  |
|
Так и хочется обратиться к ним словами поэта Гены Чера (Пр.3) : Наклоном дна течет вода, Что знает только метр. Волна бежит туда, Куда прикажет ветр. Политик, можешь ты нырять И своей ручкой дно достать? Ведь из кремлевского окна Совсем не видно дна ! Неужто ветер—хозяин твой, А ты как кораблик бежишь за волной? Ты, верно, спишь за годом год, Ужель не видишь ты теченья вод? Вода уйдет ведь все равно И сядешь ты на дно... Теперь, два слова, почему я написал эту заметку. Конечно, как и тысячи других авторов, я сам пользовался формулами Колосова сотни раз без всяких ссылок на книгу Колосова, но подтолкнул меня следующий случай. Я обратился к одному из моих русских знакомых, который считает себя знатоком истории науки и механики разрушения, с предложением ему написать что-то к столетию работы Колосова. Он сказал: «Кто такой Колосов? Вот Инглис или Броберг — это да!» Я был поражен его столь высоким мнением о заурядных ученых, решивших методом разделения переменных две простые задачи в огромных по объему статьях. (Еще будучи студентом, я дал решение задачи Броберга в функционально-инвариантных комплексных переменных на двух страницах — это решение было позже приведено в моей книге Mechanics of Brittle Fracture, McGraw Hill, New York, 1978.) Я ответил знатоку : «Броберг в подметки не годится нашему Боре Кострову (Пр.4), а Инглис—Колосову!». И сел писать эту заметку. Самоунижение и пренебрежительное отношение к своим талантливым, но не сановным ученым—старая русская болезнь. Г.П.Черепанов
август 2009 года
|  |
Перепечатка и публикация только с согласия автора. Ссылки на Веб-страницы допускаются без согласования.
© 2009. Design, комментарии. ИНКЦентр.
Оставить комментарии к настоящим материалам
E-mail to the author
The WWW-version of the essay at 2009, August 29
Обновление - ноябрь 2010.
Last updated: 2010 , November.
![]()
Форум 'Социум Экономика Право'
Форум о математикеПримечания к тексту очерка
Литературный очерк о механике разрушения и математике Г.Черепанове за 1979 г. (2009, февраль)
Так начиналась история механики разрушения в России - "Научные сражения" . (2008, ноябрь)
"В энциклопедиях не значится" - Статья Г.Черепанова из газеты "Правда" за 1984 г. (пуб. фев 2010)
Очерк о научных сражениях XXI века от Г.Черепанова (2009, октябрь)
![]()
![]() Math-Net.ru
Math-Net.ru
![]()
![]()
Комментарии
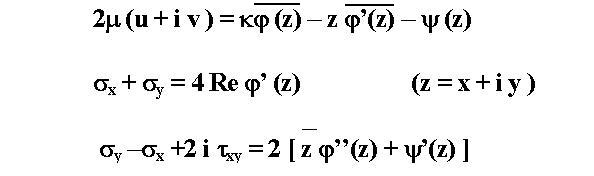
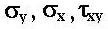 - компоненты напряжения,
- компоненты напряжения, 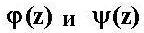 - аналитические функции комплексного переменного z (потенциалы или функции Колосова ),
- аналитические функции комплексного переменного z (потенциалы или функции Колосова ), 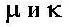 - упругие постоянные.
- упругие постоянные. 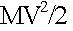 и
«мертвой силы» U(x1,x2,x3), где М — масса , V — скорость, а х1, х2, и х3 — декартовы координаты тела. Из всех возможных значений Е « в любой момент времени бог выбирает всегда самое лучшее,
т.е. максимальное, значение Е, в котором dE/dt = 0.» Отсюда, после дифференцирования следует «закон» Ньютона, который, на самом деле, является чисто эмпирическим фактом, вытекающим из широко-известного заключения Галилея, что только приложение силы вызывает изменение скорости.
и
«мертвой силы» U(x1,x2,x3), где М — масса , V — скорость, а х1, х2, и х3 — декартовы координаты тела. Из всех возможных значений Е « в любой момент времени бог выбирает всегда самое лучшее,
т.е. максимальное, значение Е, в котором dE/dt = 0.» Отсюда, после дифференцирования следует «закон» Ньютона, который, на самом деле, является чисто эмпирическим фактом, вытекающим из широко-известного заключения Галилея, что только приложение силы вызывает изменение скорости.